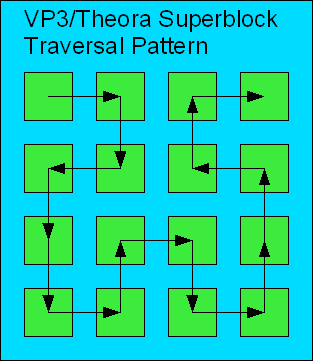
Hands down, one of the hardest parts about the VP3/Theora coding method is the bizarre fragment traversal pattern. Most everything else that VP3 does is seen in other codecs. But the Hilbert pattern used for encoding and decoding coefficients creates a monster. Vector drawing program to the rescue!

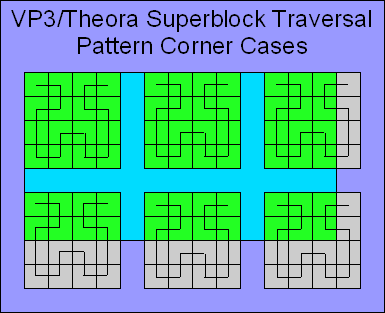
Imagine a video frame with a resolution of 96×48, highly contrived for this example. The Y plane would consist of 12×6 fragments (8×8 block of samples). Meanwhile, the U and V planes would each consist of 6×3 fragments. Recall that VP3 employs a notion of a superblock, which encompasses a group of 4×4 fragments. If the fragment resolution of a plane is not divisible by 4, the plane must be conceptually padded out to the nearest superblock boundary for the traversal pattern.

click on the image for the full sized image

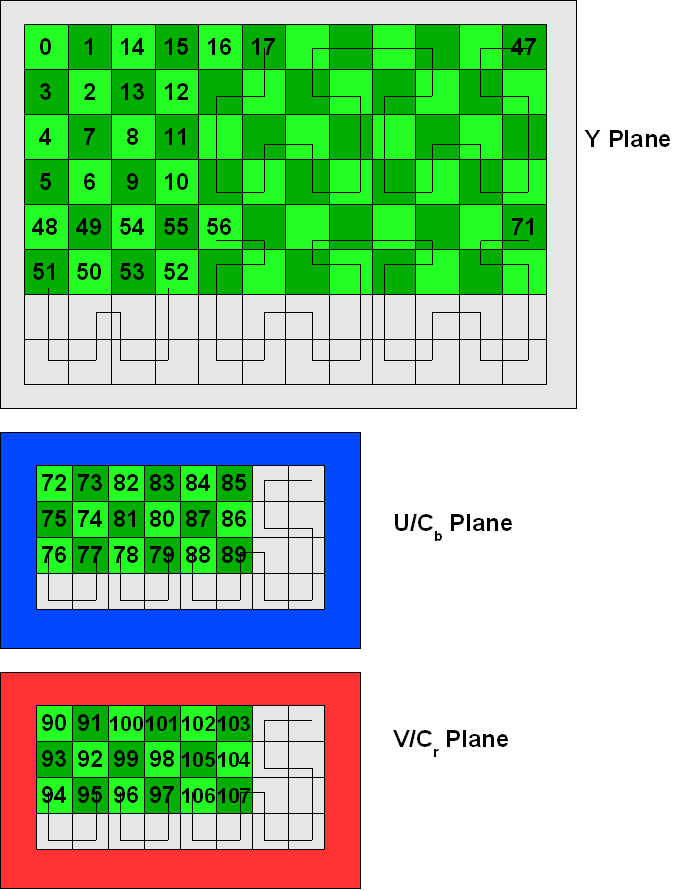
The above drawing illustrates the order that the fragments are traversed in our hypothetical 96×48 frame when decoding coefficients. Note, in particular, the strange order in which fragments 50..53 are traversed.

I hope that’s clear enough. The challenge at hand is to establish data structures at the start of the encode or decode process. Generally, you will allocate an array of fragment data structures: Fragment indices 0, 1, 2, 3, etc. will proceed left -> right, then top to bottom. The second row of the Y plane begins at index 12, third row at index 24, and so on. But when it comes to decoding the DCT coefficients, it is necessary to traverse through the fragment data structure array at indices 0, 1, 13, 12, 24, 36, 37, 25, and so on. Thus, it is customary to build an array that maps one set of indices to the other. I’m having flashbacks just thinking about it. I remember developing a completely different algorithm than the official VP3 decoder when I reimplemented the decoder for FFmpeg.

Oh yeah, and remember that all VP3/Theora decoding is performed upside-down. I choose not to illustrate that fact in these drawings since this stuff is complicated enough.

While many are still dogged by the quandary of how many licks it takes to get to the chewy center of a certain popular confection, I found myself wondering how many multiplication operations it takes to decode a frame of certain video codecs. Multiplication tends to be one of the more intensive parts of video decoding and much effort is spent minimizing the number of multiplications that are absolutely necessary. If my numbers and assumptions are correct, a 320×240 VP3/Theora intraframe requires 747,680 multiplications to decode. It goes something like this:

Each 8×8 block of the image needs to be transformed and dequantized. How many blocks are in the image?

 Y plane: (320 * 240) pixels / (8 * 8) pixels/block = 1200 blocks
 U plane: (160 * 120) pixels / (8 * 8) pixels/block =  300 blocks
 V plane: (160 * 120) pixels / (8 * 8) pixels/block =  300 blocks

So there are 1800 blocks in the frame. Each block needs to be run through an inverse discrete cosine transform (IDCT). Each of the 64 samples requires 64 mults. That means each block requires 64² mults. However, optimizations (usually by factoring out redundant mults) result in a transform that can be performed with N*log₂(N) mults.

  64 * log2(64) = 384 mults/block

This assumes that all of the blocks in the intraframe have enough non-zero coefficients that more optimal IDCTs (like 1-, 3-, and 10-element) are not warranted. Then there is the matter of dequantization. Assuming an average of 16 non-zero coefficients in need of dequantization, the number of mults per block rises to 400.

 400 mults/block * 1800 blocks/frame = 720000 mults/frame

The same number would hold true for JPEG images or MPEG-1 intraframes, given the same (possibly fraudulent) assumptions. I am not sure if 16 non-zero coefficients per block is too generous and too conservative an estimate. However, the vast majority of the blocks in a VP3/Theora intraframe will also require 3 multiplications in order to reverse the DC prediction. So I’ll just wave my hand and factor DC prediction in with the dequantization budget of 16 mults/block.

Now, if we want to deploy the recommended post processing method, that requires 8 more multiplications per edge, where ‘edge’ is a boundary between 2 blocks that have been rendered in this frame (and all blocks are rendered for an intraframe). How many edges are in the frame?

• vertical edges = (width_in_blocks – 1) * (height_in_blocks)
• horizontal edges = (width_in_blocks) * (height_in_blocks – 1)

 Y plane: 40x30 blocks, (40 - 1) * 30 + 40 * (30 - 1) = 1170 + 1160 = 2330 edges
 U plane: 20x15 blocks, (20 - 1) * 15 + 20 * (15 - 1) =  285 +  280 =  565 edges
 V plane: 20x15 blocks, (20 - 1) * 15 + 20 * (15 - 1) =  285 +  280 =  565 edges
 
 3460 edges/frame * 8 PP mults/edge = 27680 PP mults/frame

Thus:

 720000 mults/frame + 27680 mults/frame = 747680 mults/frame

It should be noted that VP3/Theora’s method for post-processing involves a 4-tap filter with coefficients of (1, -1, 3, -3). Trivially, the multiplication by 3 can be factored out (which is how the assumption of one mult per sample, or 8 per edge, is derived). Further, it can easily be broken down to a bit shift and addition (3*n = (n << 1) + n) so that the post processing phase does not strictly require any multiplications. Naturally, the parameters for a nominal VP3/Theora interframe vary wildly and it's a little harder to produce an average number of multiplications for that case. I'm sure someone will be along in the comments if I messed up the math or, more likely, the assumptions.